Avis au lecteur: ceci est une prise de note pour moi même. Pas très simple à lire, voire pénible.
Pourquoi au jeu de l’oie, quand le premier joueur fait un 5 et un 4 il doit aller sur la case 53 et quand il fait un 6 et un 3 il doit aller case 26 ?
Telle est la question qui tracasse les petits pois ce soir…
Parce que la réponse qui consiste à dire que sur la case 54 (6×9) ou 45 (5×9) il y a une oie et du coup de 9 en 9 tranquillement on arriverai au 63 et pareil pour la case 36 (4×9) et ne parlons pas de la case 63 (7×9) … ben ça ne suffit pas aux petits pois.
Parce que cette réponse ne justifie pas les cases 53 et 26, elle ne fait qu’éliminer les cases 45, 54 et 36 et 63.
D’ailleurs, en réalité, on aurait pu tout aussi bien éliminer les cases: 5, 9, 14, 18, 23, 27,32, (36), 41, (45), 50, (54), 59 et (63) qui sont toutes les cases sur lesquelles sont posées une oie.
Ajoutons à cela que les cases 12/6 ,19 ,31 ,42/30 , 52 et 58/1 ont leur règle propre, et cela fait d’autant plus de cases à éliminer.
Mais ça laissait quand même pas mal de choix au(x) concepteur(s) du jeu:
2, 3, 4, 7, 8, 10, 11, 13, 15, 16, 17, 20, 21, 22, 24, 25, 26, 28, 29, 33, 34, 35, 37, 38, 39, 40, 43, 44, 46, 47, 48, 49, 51, 53, 54, 55, 56, 57, 60, 61 et 62
Et parmi toutes ces cases, ils ont choisis 53 pour 5 et 4 et 26 pour 3 et 6…
Pourquoi ?
A celui qui dit que la case 53 est la plus proche du 54, je peux rétorquer:
- la 55 est tout aussi proche
- pourquoi dans ce cas prendre 26 et pas 35 (si on suit la logique précédente) pour un 3 et un 6
Et dans le sens inverse, s’il s’agit d’enlever 10 à 36 pour arriver à la case 26, pourquoi alors ne pas avoir enlever 10 à 54 ? La case 44 était également disponible.
J’ai trouvé peu, très peu de personnes que cette question a effleuré…
En fait, juste un.
Un certain M. Aimé Mariage qui pense que le jeu de l’oie est une preuve de la numération octale (octovale?)chez le Grecs…

Et une analyse du texte de M. Mariage sur le site http://academiedesjeux.jeuxsoc.fr
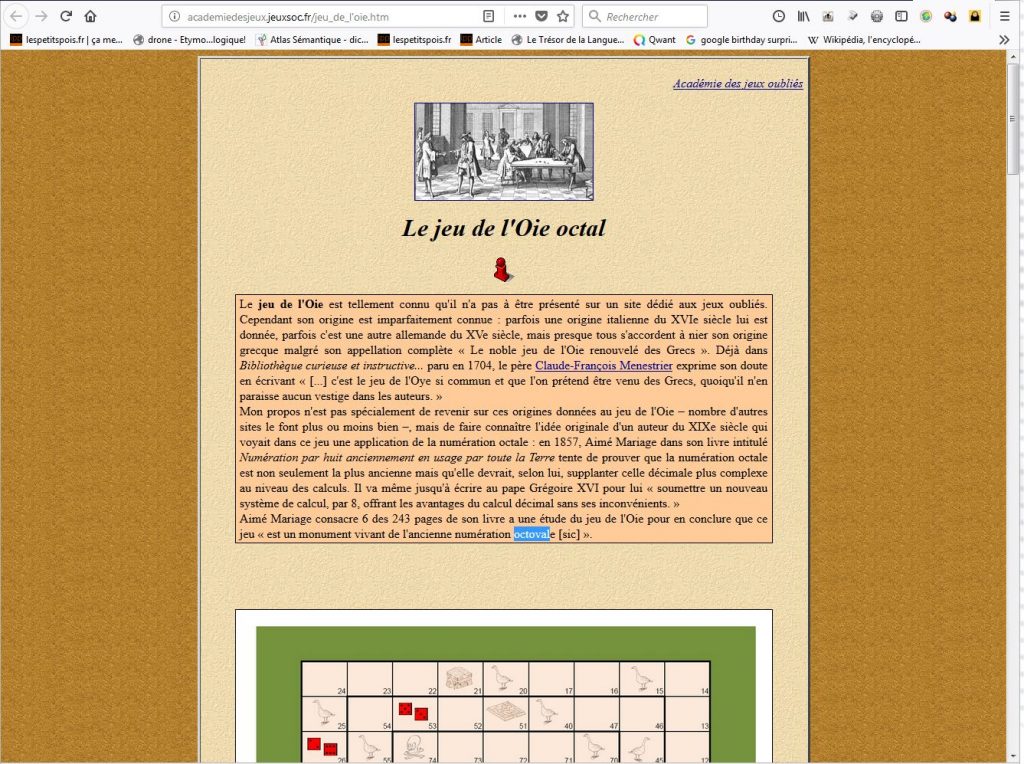
Bref, intéressant, mais pas probant.
J’ai essayé plusieurs choses.
Par exemple, pour rester sur cette idée de changer de système de numération, savez-vous qu’en duodécimal, 53 s’écrit 45 (un 4 et un 5, comme le tirage !). Mais ça ne marche évidemment pas avec 36 qui s’écrit 30. Ben ouais, dommage.
Et le seul “truc” qui fonctionne sans pour autant tout expliquer est le suivant:
(case) 53 (tirage 5 et 4) est la somme des 5 nombres premiers suivants: 5 + 7 + 11 + 13 + 17
=> Soit 5 + les 4 nombres premiers qui suivent
Tandis que (case) 26 (tirage 3 et 6) est la somme des 4 nombres premiers 3 + 5 + 7 + 11
=> Mais on a pas la même logique encore une fois sur le 26 que précédemment sur le 53; en effet, pourquoi s’arrêter au 3 chiffres qui suivent le 3 et ne pas aller jusqu’au 6ème nombre premier ? Ne vous en faite pas, c’est à moi que je pose la question. Et là je répond: ben tout bonnement parce que la somme des ces nombres premiers fait 75 ( 3+5+7+11+13+17+19,) ce qui dépasse largement le nombre de case du jeu de L’oie – 63 -.
… – soupir –
Pour le moment, je suis au bout de ma réflexion sur ce sujet. Si vous avez des idées exploitables, l’espace commentaire est à vous. Surtout ne vous privez pas !